
Compas de proportion, XVIIe s., inv. 3076
l=20 cm
© Musées royaux d’Art et d’Histoire
Portfolio :


Le compas de proportion est composé de deux règles, généralement en laiton ou une autre matière solide, reliées à une de leurs extrémités par une charnière. Sa longueur est généralement de 6 pouces (=1/2 pied=15,24 cm). Chacune des règles porte une série de lignes. Toutes les lignes sont identiques deux à deux et partent du centre de la charnière pour diverger de manière symétrique par rapport à l’axe d’ouverture du compas. Ces lignes ont chacune leur propre graduation. Ainsi, il permettait de calculer des proportions, de réaliser des figures homothétiques, mesurer des angles, des arcs, …
Qui ?
L’invention du compas de proportion a été attribuée à Galilée (1564-1642) en 1606 (date de publication de son traité Operazioni del compasso geometrico e militare) mais cette idée a été remise en question. Le premier exemplaire aurait peut-être été inventé par Guidobaldo del Monte (1545-1607) en 1568. Le nom de l’Anversois Michel Coignet (1549-1623) a aussi été cité.
Quand ?
Le compas de proportion est un instrument de mathématique et de géométrie très utilisé du XVIIe au XIXe siècle.
Évolution :
Le compas de Guidobaldo del Monte comportait seulement quelques lignes et se terminait par des pointes. Galilée l’améliore, mais les compas ultérieurs seront plus simples que le sien.
Le compas de proportion a été fabriqué en Angleterre, en France et en Italie. Il a servi aux géomètres, aux architectes, aux négociants, aux navigateurs, aux artilleurs et à bien d’autres professions.
Pour quoi ?
Il sert à connaître les proportions des quantités de même espèce, d’où l’origine de son nom. Il permettait de faciliter les calculs trop lourds pour l’être humain, à la manière de la calculatrice et même de l’ordinateur. Ses utilisations étaient très diverses, c’est pourquoi beaucoup de gens l’utilisaient, tels les géomètres, les architectes, les négociants, les navigateurs et bien d’autres personnes. Il est impossible d’expliquer toutes les utilisations de cet instrument car celles-ci étaient différentes selon les lieux d’où il venait et selon la profession à laquelle il était destiné.
Comment ?
Le principe de base de l’utilisation du compas de proportion est celui des triangles semblables (note : Triangles dont les côtés sont proportionnels et dont les angles sont les mêmes. Lorsqu’un triangle est sectionné par une droite parallèle à l’un des cotés de ce triangle, il se forme deux triangles semblables dont le rapport des côtés homologues est le même).
Usage de la ligne des parties égales :
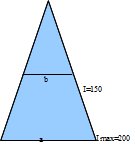
I = valeur qui accompagne la graduation de la ligne des parties égales.
I max= la valeur maximale que peut avoir I. On souhaite par exemple dessiner une piscine ronde sur un plan dont le diamètre est égal à 3/4a. On prend un compas à pointe sèche et on relève sur le plan la longueur du diamètre de longueur a. On ouvre le compas de proportion de manière à ce que l’écartement des deux jambes soit égal à la longueur relevée par l’autre compas à la graduation de I max. On considère que le compas de proportion que nous possédons a un I max de 200. On peut donc trouver la longueur 3/4a de cette manière :
I/Imax= 3/4 => I/200 = 3/4
I= 150
On relève avec l’écartement des deux jambes à l’aide d’un compas à pointe sèche à la hauteur de la graduation I max et on le reporte sur notre plan à l’endroit où l’on voulait qu’il soit.
Usage de la ligne des plans :
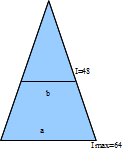
On reprend la même situation qu’au dessus mais on veut que les surfaces des deux piscines aient un rapport de 3/4.
Cette fois-ci I max est égal à 64. On relève comme à l’exemple précédent la longueur de a à l’aide d’un compas à pointe sèche et on écarte le compas d’une longueur de a entre les graduations de 64.On peut trouver la longueur de b de cette manière :
I/I max = 3/4 => I/64 = 3/4
I=48
On relève la longueur de b à la graduation I=48 avec un compas à pointe sèche. Cette longueur est de √3/4 a car nous sommes dans un rapport de surface. On reporte la longueur de b à l’endroit désiré sur le plan. On peut donc remarquer que la surface de la piscine de diamètre a est :
Π(a/2)2 ≈ 0,7854a2
La surface de la piscine de diamètre b est :
Π(√3/4/2)2 ≈ 0,5890a2
=> La piscine de diamètre a est bien d’aire égale à celle de la piscine de diamètre b si on la multiplie par 3/4.
Œuvres liées :
Références :
D’ALEMBERT J., DE LA LANDE J., L’ABBE BOSSUT, Encyclopédie Méthodique Mathématiques, Paris, Panckoucke, 1784.
BAVEREL D., « Le compas de proportion », Instruments scientifiques à travers l’Histoire, ss dir. E. HEBERT, Paris, 2004, p. 315-336.
CHINA M., Les compas de proportion, association des amis du musée géo-expert de la région Rône-Alpes, géomusée, (Page consultée le 28 janvier 2012).
DAUMAS M., Les instruments scientifiques aux XVIIe et XVIIIe siècles, Paris, 1953, p. 33-36.
MICHEL H., Instruments des sciences dans l’art et l’histoire, Rhode-St-Genèse, 1980, p. 22.
OZANAM J., L’usage du compas de proportion expliqué et démontré d’une manière courte et facile et augmenté d’un Traité de la division des champs, Paris, Estienne Michallet, 1688.
http://fr.wikipedia.org/wiki/Michel_Coignet
http://fr.wikipedia.org/wiki/Guidobaldo_del_Monte
















